How To Describe The Moon

Laws describing the motion of planets

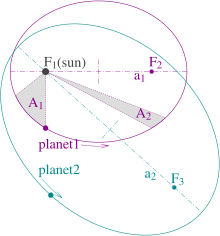
Figure 1: Illustration of Kepler'southward three laws with two planetary orbits.

1. The orbits are ellipses, with focal points F ₁ and F _ii for the first planet and F _ane and F ₃ for the 2d planet. The Sun is placed at focal point F ₁.
2. The 2 shaded sectors A _one and A _ii accept the aforementioned surface surface area and the time for planet 1 to cover segment A _i is equal to the time to cover segment A ₂.
3. The total orbit times for planet 1 and planet 2 have a ratio ${\textstyle \left({\frac {a_{one}}{a_{ii}}}\correct)^{\frac {3}{ii}}}$ .

In astronomy, Kepler'south laws of planetary motion, published by Johannes Kepler between 1609 and 1619, describe the orbits of planets around the Sun. The laws modified the heliocentric theory of Nicolaus Copernicus, replacing its circular orbits and epicycles with elliptical trajectories, and explaining how planetary velocities vary. The three laws state that:

1. The orbit of a planet is an ellipse with the Sunday at one of the two foci.
2. A line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time.
3. The square of a planet's orbital period is proportional to the cube of the length of the semi-major axis of its orbit.

The elliptical orbits of planets were indicated by calculations of the orbit of Mars. From this, Kepler inferred that other bodies in the Solar System, including those farther abroad from the Sun, also have elliptical orbits. The 2nd law helps to institute that when a planet is closer to the Dominicus, it travels faster. The third constabulary expresses that the farther a planet is from the Sun, the slower its orbital speed, and vice versa.

Isaac Newton showed in 1687 that relationships like Kepler'due south would employ in the Solar System as a consequence of his own laws of movement and police force of universal gravitation.

Comparison to Copernicus [edit]

Johannes Kepler's laws improved the model of Copernicus. If the eccentricities of the planetary orbits are taken equally zero, then Kepler basically agreed with Copernicus:

1. The planetary orbit is a circumvolve with epicycles.
2. The Sun is approximately at the middle of the orbit.
3. The speed of the planet in the principal orbit is constant.

The eccentricities of the orbits of those planets known to Copernicus and Kepler are small-scale, so the foregoing rules requite fair approximations of planetary movement, but Kepler's laws fit the observations better than does the model proposed by Copernicus. Kepler'southward corrections are:

1. The planetary orbit is not a circle with epicycles, but an ellipse.
2. The Sun is not near the center but at a focal betoken of the elliptical orbit.
3. Neither the linear speed nor the athwart speed of the planet in the orbit is abiding, but the area speed (closely linked historically with the concept of angular momentum) is constant.

The eccentricity of the orbit of the Earth makes the fourth dimension from the March equinox to the September equinox, around 186 days, unequal to the time from the September equinox to the March equinox, around 179 days. A diameter would cut the orbit into equal parts, merely the plane through the Sunday parallel to the equator of the Earth cuts the orbit into ii parts with areas in a 186 to 179 ratio, and then the eccentricity of the orbit of the Earth is approximately

${\displaystyle e\approx {\frac {\pi }{four}}{\frac {186-179}{186+179}}\approx 0.015,}$

which is close to the right value (0.016710218). The accuracy of this calculation requires that the two dates chosen be along the elliptical orbit'south modest axis and that the midpoints of each half exist along the major centrality. As the ii dates chosen here are equinoxes, this will be correct when perihelion, the date the Globe is closest to the Sunday, falls on a solstice. The current perihelion, near January iv, is adequately shut to the solstice of Dec 21 or 22.

Nomenclature [edit]

It took nearly two centuries for current formulation of Kepler's work to accept on its settled class. Voltaire'southward Eléments de la philosophie de Newton (Elements of Newton'southward Philosophy) of 1738 was the showtime publication to utilise the terminology of "laws".^{[i] [2]} The Biographical Encyclopedia of Astronomers in its article on Kepler (p. 620) states that the terminology of scientific laws for these discoveries was electric current at least from the time of Joseph de Lalande.^[iii] It was the exposition of Robert Small, in An business relationship of the astronomical discoveries of Kepler (1814) that made up the set of three laws, by adding in the third.^[iv] Minor also claimed, against the history, that these were empirical laws, based on inductive reasoning.^{[2] [v]}

Farther, the current usage of "Kepler's Second Law" is something of a misnomer. Kepler had ii versions, related in a qualitative sense: the "distance constabulary" and the "expanse law". The "expanse law" is what became the Second Constabulary in the set of 3; but Kepler did himself not privilege it in that way.^[6]

History [edit]

Kepler published his commencement two laws about planetary motility in 1609,^[seven] having constitute them by analyzing the astronomical observations of Tycho Brahe.^{[viii] [ix] [10]} Kepler's third police force was published in 1619.^{[11] [nine]} Kepler had believed in the Copernican model of the Solar Organization, which called for circular orbits, just he could non reconcile Brahe'south highly precise observations with a circular fit to Mars' orbit – Mars coincidentally having the highest eccentricity of all planets except Mercury.^[12] His first law reflected this discovery.

In 1621, Kepler noted that his 3rd law applies to the 4 brightest moons of Jupiter.^{[Nb 1]} Godefroy Wendelin as well made this observation in 1643.^{[Nb two]} The second law, in the "area law" course, was contested by Nicolaus Mercator in a book from 1664, but by 1670 his Philosophical Transactions were in its favour.^{[13] [14]} Every bit the century proceeded it became more widely accustomed.^[15] The reception in Federal republic of germany changed noticeably between 1688, the year in which Newton'southward Principia was published and was taken to be basically Copernican, and 1690, by which time work of Gottfried Leibniz on Kepler had been published.^[xvi]

Newton was credited with understanding that the 2d constabulary is not special to the inverse foursquare police of gravitation, being a outcome just of the radial nature of that law, whereas the other laws do depend on the changed square class of the attraction. Carl Runge and Wilhelm Lenz much later identified a symmetry principle in the phase space of planetary motility (the orthogonal group O(4) acting) which accounts for the showtime and 3rd laws in the example of Newtonian gravitation, every bit conservation of angular momentum does via rotational symmetry for the second police force.^[17]

Formulary [edit]

The mathematical model of the kinematics of a planet subject to the laws allows a large range of further calculations.

First law [edit]

The orbit of every planet is an ellipse with the Sunday at one of the two foci.

Effigy ii: Kepler's start law placing the Sunday at the focus of an elliptical orbit

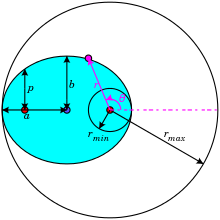
Figure 3: Heliocentric coordinate system (r, θ) for ellipse. Likewise shown are: semi-major axis a, semi-minor axis b and semi-latus rectum p; center of ellipse and its two foci marked by large dots. For θ = 0°, r = r _min and for θ = 180°, r = r _max .

Mathematically, an ellipse can be represented by the formula:

${\displaystyle r={\frac {p}{1+\varepsilon \,\cos \theta }},}$

where ${\displaystyle p}$ is the semi-latus rectum, ε is the eccentricity of the ellipse, r is the altitude from the Sun to the planet, and θ is the angle to the planet'due south current position from its closest approach, as seen from the Sun. And so (r,θ) are polar coordinates.

For an ellipse 0 <ε < 1 ; in the limiting case ε = 0, the orbit is a circle with the Sun at the centre (i.e. where at that place is zilch eccentricity).

At θ = 0°, perihelion, the altitude is minimum

${\displaystyle r_{\min }={\frac {p}{1+\varepsilon }}}$

At θ = 90° and at θ = 270° the distance is equal to ${\displaystyle p}$ .

At θ = 180°, aphelion, the altitude is maximum (past definition, aphelion is – invariably – perihelion plus 180°)

${\displaystyle r_{\max }={\frac {p}{ane-\varepsilon }}}$

The semi-major axis a is the arithmetic mean betwixt r _min and r _max:

${\displaystyle {\brainstorm{aligned}r_{\max }-a&=a-r_{\min }\\[3pt]a&={\frac {p}{1-\varepsilon ^{ii}}}\end{aligned}}}$

The semi-pocket-size axis b is the geometric hateful between r _min and r _max:

${\displaystyle {\begin{aligned}{\frac {r_{\max }}{b}}&={\frac {b}{r_{\min }}}\\[3pt]b&={\frac {p}{\sqrt {1-\varepsilon ^{two}}}}\stop{aligned}}}$

The semi-latus rectum p is the harmonic mean betwixt r _min and r _max:

${\displaystyle {\begin{aligned}{\frac {1}{r_{\min }}}-{\frac {i}{p}}&={\frac {1}{p}}-{\frac {1}{r_{\max }}}\\[3pt]pa&=r_{\max }r_{\min }=b^{2}\,\end{aligned}}}$

The eccentricity ε is the coefficient of variation between r _min and r _max:

${\displaystyle \varepsilon ={\frac {r_{\max }-r_{\min }}{r_{\max }+r_{\min }}}.}$

The area of the ellipse is

${\displaystyle A=\pi ab\,.}$

The special instance of a circumvolve is ε = 0, resulting in r = p = r _min = r _max = a = b and A = πr ².

2nd constabulary [edit]

A line joining a planet and the Sun sweeps out equal areas during equal intervals of time.^[xviii]

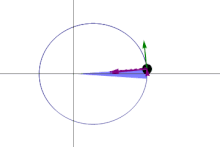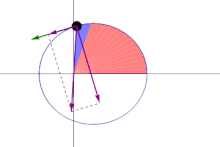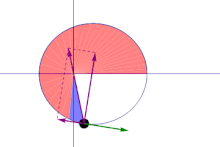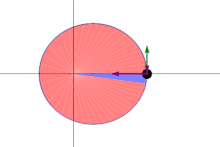
The same (blueish) area is swept out in a stock-still time period. The green arrow is velocity. The purple arrow directed towards the Sun is the acceleration. The other two royal arrows are dispatch components parallel and perpendicular to the velocity.

The orbital radius and athwart velocity of the planet in the elliptical orbit volition vary. This is shown in the animation: the planet travels faster when closer to the Sun, and then slower when farther from the Sun. Kepler's second law states that the blueish sector has constant area.

In a pocket-size time ${\displaystyle dt}$ the planet sweeps out a small triangle having base of operations line ${\displaystyle r}$ and height ${\displaystyle r\,d\theta }$ and expanse ${\textstyle dA={\frac {1}{2}}\cdot r\cdot r\,d\theta }$ , so the constant areal velocity is

$${\displaystyle {\frac {dA}{dt}}={\frac {r^{2}}{2}}{\frac {d\theta }{dt}}.}$$

The area enclosed by the elliptical orbit is ${\displaystyle \pi ab}$ . So the period ${\displaystyle T}$ satisfies

${\displaystyle T\cdot {\frac {r^{2}}{2}}{\frac {d\theta }{dt}}=\pi ab}$

and the hateful movement of the planet around the Sun

${\displaystyle due north={\frac {2\pi }{T}}}$

satisfies

${\displaystyle r^{2}\,d\theta =abn\,dt.}$

And so,

$${\displaystyle {\frac {dA}{dt}}={\frac {abn}{2}}={\frac {\pi ab}{T}}.}$$

Orbits of planets with varying eccentricities. The cherry-red ray rotates at a constant angular velocity and with the same orbital time period as the planet, ${\displaystyle T=i}$ . S: Sun at the main focus, C: Centre of ellipse, Southward': The secondary focus. In each example, the surface area of all sectors depicted is identical.

Low	High
Planet orbiting the Sun in a circular orbit (due east=0.0)	Planet orbiting the Sun in an orbit with due east=0.five
Planet orbiting the Sun in an orbit with e=0.2	Planet orbiting the Sun in an orbit with eastward=0.eight

Third law [edit]

The ratio of the square of an object's orbital flow with the cube of the semi-major axis of its orbit is the aforementioned for all objects orbiting the same primary.

This captures the relationship betwixt the distance of planets from the Sun, and their orbital periods.

Kepler enunciated in 1619^[11] this tertiary law in a laborious try to determine what he viewed as the "music of the spheres" co-ordinate to precise laws, and express information technology in terms of musical notation.^[19] Information technology was therefore known equally the harmonic law.^[20]

Using Newton's law of gravitation (published 1687), this relation can be institute in the example of a round orbit past setting the centripetal force equal to the gravitational force:

${\displaystyle mr\omega ^{2}=G{\frac {mM}{r^{2}}}}$

And then, expressing the angular velocity ω in terms of the orbital period ${\displaystyle {T}}$ and and so rearranging, results in Kepler's Tertiary Constabulary:

${\displaystyle mr\left({\frac {2\pi }{T}}\correct)^{2}=G{\frac {mM}{r^{2}}}\rightarrow T^{2}=\left({\frac {iv\pi ^{2}}{GM}}\right)r^{3}\rightarrow T^{ii}\propto r^{3}}$

A more detailed derivation can be done with general elliptical orbits, instead of circles, besides as orbiting the middle of mass, instead of simply the big mass. This results in replacing a circular radius, ${\displaystyle r}$ , with the semi-major axis, ${\displaystyle a}$ , of the elliptical relative movement of 1 mass relative to the other, likewise as replacing the large mass ${\displaystyle M}$ with ${\displaystyle M+m}$ . Nevertheless, with planet masses existence so much smaller than the Sun, this correction is often ignored. The full corresponding formula is:

${\displaystyle {\frac {a^{3}}{T^{ii}}}={\frac {G(M+grand)}{4\pi ^{2}}}\approx {\frac {GM}{four\pi ^{2}}}\approx 7.496\times 10^{-6}{\frac {{\text{AU}}^{3}}{{\text{days}}^{2}}}{\text{ is constant}}}$

where ${\displaystyle M}$ is the mass of the Sunday, ${\displaystyle yard}$ is the mass of the planet, ${\displaystyle G}$ is the gravitational constant, ${\displaystyle T}$ is the orbital period and ${\displaystyle a}$ is the elliptical semi-major axis, and ${\displaystyle {\text{AU}}}$ is the astronomical unit, the average distance from earth to the sun.

The following tabular array shows the data used by Kepler to empirically derive his constabulary:

Data used by Kepler (1618)

Planet	Mean altitude to sun (AU)	Period (days)	${\textstyle {\frac {R^{three}}{T^{2}}}}$ (x-half dozen AU3/24-hour interval2)
Mercury	0.389	87.77	seven.64
Venus	0.724	224.70	vii.52
Earth	1	365.25	seven.50
Mars	1.524	686.95	7.50
Jupiter	five.20	4332.62	seven.49
Saturn	ix.510	10759.2	7.43

Upon finding this pattern Kepler wrote:^[21]

I kickoff believed I was dreaming... But it is absolutely certain and exact that the ratio which exists betwixt the period times of whatever ii planets is precisely the ratio of the three/2th ability of the mean altitude.

—translated from Harmonies of the Globe past Kepler (1619)

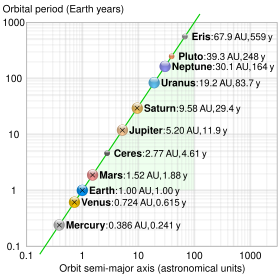
Log-log plot of period T vs semi-major axis a (average of aphelion and perihelion) of some Solar System orbits (crosses denoting Kepler'south values) showing that a³/T² is constant (green line)

For comparing, here are modern estimates:

Modern information (Wolfram Blastoff Knowledgebase 2018)

Planet	Semi-major centrality (AU)	Menses (days)	${\textstyle {\frac {R^{iii}}{T^{2}}}}$ (10-6 AU3/day2)
Mercury	0.38710	87.9693	7.496
Venus	0.72333	224.7008	vii.496
Earth	1	365.2564	7.496
Mars	one.52366	686.9796	vii.495
Jupiter	5.20336	4332.8201	7.504
Saturn	9.53707	10775.599	7.498
Uranus	19.1913	30687.153	7.506
Neptune	30.0690	60190.03	vii.504

Planetary dispatch [edit]

Isaac Newton computed in his Philosophiæ Naturalis Principia Mathematica the dispatch of a planet moving according to Kepler's outset and 2d laws.

1. The direction of the dispatch is towards the Dominicus.
2. The magnitude of the acceleration is inversely proportional to the square of the planet's altitude from the Sun (the inverse square law).

This implies that the Dominicus may exist the concrete cause of the acceleration of planets. However, Newton states in his Principia that he considers forces from a mathematical bespeak of view, not a concrete, thereby taking an instrumentalist view.^[22] Moreover, he does not assign a cause to gravity.^[23]

Newton defined the strength interim on a planet to exist the product of its mass and the acceleration (come across Newton'due south laws of motion). So:

1. Every planet is attracted towards the Sun.
2. The force acting on a planet is straight proportional to the mass of the planet and is inversely proportional to the square of its distance from the Sun.

The Sun plays an unsymmetrical function, which is unjustified. So he causeless, in Newton's constabulary of universal gravitation:

1. All bodies in the Solar System attract i another.
2. The force between two bodies is in direct proportion to the product of their masses and in changed proportion to the square of the distance between them.

Every bit the planets have pocket-size masses compared to that of the Sun, the orbits suit approximately to Kepler's laws. Newton'due south model improves upon Kepler's model, and fits actual observations more accurately. (See two-torso problem.)

Below comes the detailed calculation of the acceleration of a planet moving co-ordinate to Kepler's first and second laws.

Acceleration vector [edit]

From the heliocentric bespeak of view consider the vector to the planet ${\displaystyle \mathbf {r} =r{\hat {\mathbf {r} }}}$ where ${\displaystyle r}$ is the altitude to the planet and ${\displaystyle {\lid {\mathbf {r} }}}$ is a unit vector pointing towards the planet.

$${\displaystyle {\frac {d{\lid {\mathbf {r} }}}{dt}}={\dot {\chapeau {\mathbf {r} }}}={\dot {\theta }}{\hat {\boldsymbol {\theta }}},\qquad {\frac {d{\hat {\boldsymbol {\theta }}}}{dt}}={\dot {\hat {\boldsymbol {\theta }}}}=-{\dot {\theta }}{\chapeau {\mathbf {r} }}}$$

where ${\displaystyle {\hat {\boldsymbol {\theta }}}}$ is the unit vector whose direction is 90 degrees counterclockwise of ${\displaystyle {\hat {\mathbf {r} }}}$ , and ${\displaystyle \theta }$ is the polar bending, and where a dot on pinnacle of the variable signifies differentiation with respect to time.

Differentiate the position vector twice to obtain the velocity vector and the acceleration vector:

$${\displaystyle {\brainstorm{aligned}{\dot {\mathbf {r} }}&={\dot {r}}{\hat {\mathbf {r} }}+r{\dot {\hat {\mathbf {r} }}}={\dot {r}}{\hat {\mathbf {r} }}+r{\dot {\theta }}{\chapeau {\boldsymbol {\theta }}},\\{\ddot {\mathbf {r} }}&=\left({\ddot {r}}{\lid {\mathbf {r} }}+{\dot {r}}{\dot {\lid {\mathbf {r} }}}\right)+\left({\dot {r}}{\dot {\theta }}{\hat {\boldsymbol {\theta }}}+r{\ddot {\theta }}{\lid {\boldsymbol {\theta }}}+r{\dot {\theta }}{\dot {\hat {\boldsymbol {\theta }}}}\correct)=\left({\ddot {r}}-r{\dot {\theta }}^{2}\right){\lid {\mathbf {r} }}+\left(r{\ddot {\theta }}+2{\dot {r}}{\dot {\theta }}\right){\hat {\boldsymbol {\theta }}}.\end{aligned}}}$$

Then

$${\displaystyle {\ddot {\mathbf {r} }}=a_{r}{\hat {\boldsymbol {r}}}+a_{\theta }{\chapeau {\boldsymbol {\theta }}}}$$

where the radial dispatch is

$${\displaystyle a_{r}={\ddot {r}}-r{\dot {\theta }}^{ii}}$$

and the transversal acceleration is

$${\displaystyle a_{\theta }=r{\ddot {\theta }}+2{\dot {r}}{\dot {\theta }}.}$$

Inverse square law [edit]

Kepler'due south second police says that

$${\displaystyle r^{2}{\dot {\theta }}=nab}$$

is constant.

The transversal acceleration ${\displaystyle a_{\theta }}$ is naught:

$${\displaystyle {\frac {d\left(r^{2}{\dot {\theta }}\right)}{dt}}=r\left(2{\dot {r}}{\dot {\theta }}+r{\ddot {\theta }}\right)=ra_{\theta }=0.}$$

So the acceleration of a planet obeying Kepler's second law is directed towards the Sunday.

The radial acceleration ${\displaystyle a_{\text{r}}}$ is

$${\displaystyle a_{\text{r}}={\ddot {r}}-r{\dot {\theta }}^{2}={\ddot {r}}-r\left({\frac {nab}{r^{2}}}\right)^{two}={\ddot {r}}-{\frac {n^{2}a^{2}b^{2}}{r^{3}}}.}$$

Kepler'south start law states that the orbit is described past the equation:

$${\displaystyle {\frac {p}{r}}=i+\varepsilon \cos(\theta ).}$$

Differentiating with respect to time

$${\displaystyle -{\frac {p{\dot {r}}}{r^{ii}}}=-\varepsilon \sin(\theta )\,{\dot {\theta }}}$$

or

$${\displaystyle p{\dot {r}}=nab\,\varepsilon \sin(\theta ).}$$

Differentiating once more

$${\displaystyle p{\ddot {r}}=nab\varepsilon \cos(\theta )\,{\dot {\theta }}=nab\varepsilon \cos(\theta )\,{\frac {nab}{r^{two}}}={\frac {north^{ii}a^{two}b^{2}}{r^{two}}}\varepsilon \cos(\theta ).}$$

The radial acceleration ${\displaystyle a_{\text{r}}}$ satisfies

$${\displaystyle pa_{\text{r}}={\frac {n^{two}a^{2}b^{2}}{r^{2}}}\varepsilon \cos(\theta )-p{\frac {due north^{2}a^{2}b^{2}}{r^{3}}}={\frac {n^{2}a^{2}b^{2}}{r^{2}}}\left(\varepsilon \cos(\theta )-{\frac {p}{r}}\right).}$$

Substituting the equation of the ellipse gives

$${\displaystyle pa_{\text{r}}={\frac {n^{2}a^{ii}b^{2}}{r^{ii}}}\left({\frac {p}{r}}-1-{\frac {p}{r}}\right)=-{\frac {n^{2}a^{two}}{r^{2}}}b^{ii}.}$$

The relation ${\displaystyle b^{ii}=pa}$ gives the uncomplicated last event

$${\displaystyle a_{\text{r}}=-{\frac {northward^{2}a^{3}}{r^{2}}}.}$$

This means that the acceleration vector ${\displaystyle \mathbf {\ddot {r}} }$ of whatsoever planet obeying Kepler's first and 2d law satisfies the inverse square law

$${\displaystyle \mathbf {\ddot {r}} =-{\frac {\alpha }{r^{2}}}{\chapeau {\mathbf {r} }}}$$

where

$${\displaystyle \alpha =northward^{ii}a^{3}}$$

is a constant, and ${\displaystyle {\chapeau {\mathbf {r} }}}$ is the unit vector pointing from the Dominicus towards the planet, and ${\displaystyle r\,}$ is the altitude between the planet and the Sun.

Since mean motion ${\displaystyle due north={\frac {2\pi }{T}}}$ where ${\displaystyle T}$ is the period, according to Kepler's third law, ${\displaystyle \alpha }$ has the same value for all the planets. So the inverse square law for planetary accelerations applies throughout the entire Solar Arrangement.

The changed square law is a differential equation. The solutions to this differential equation include the Keplerian motions, as shown, only they also include motions where the orbit is a hyperbola or parabola or a directly line. (Encounter Kepler orbit.)

Newton'south law of gravitation [edit]

Past Newton's second law, the gravitational strength that acts on the planet is:

$${\displaystyle \mathbf {F} =m_{\text{planet}}\mathbf {\ddot {r}} =-m_{\text{planet}}\alpha r^{-2}{\lid {\mathbf {r} }}}$$

where ${\displaystyle m_{\text{planet}}}$ is the mass of the planet and ${\displaystyle \blastoff }$ has the same value for all planets in the Solar Organisation. According to Newton'south third law, the Sun is attracted to the planet by a forcefulness of the same magnitude. Since the force is proportional to the mass of the planet, under the symmetric consideration, it should also be proportional to the mass of the Sun, ${\displaystyle m_{\text{Sun}}}$ . And so

$${\displaystyle \alpha =Gm_{\text{Sunday}}}$$

where ${\displaystyle G}$ is the gravitational constant.

The acceleration of solar system body number i is, co-ordinate to Newton'southward laws:

$${\displaystyle \mathbf {\ddot {r}} _{i}=G\sum _{j\neq i}m_{j}r_{ij}^{-2}{\hat {\mathbf {r} }}_{ij}}$$

where ${\displaystyle m_{j}}$ is the mass of torso j, ${\displaystyle r_{ij}}$ is the distance between body i and body j, ${\displaystyle {\lid {\mathbf {r} }}_{ij}}$ is the unit vector from body i towards torso j, and the vector summation is over all bodies in the Solar Arrangement, as well i itself.

In the special case where there are simply 2 bodies in the Solar System, Earth and Sunday, the acceleration becomes

$${\displaystyle \mathbf {\ddot {r}} _{\text{Earth}}=Gm_{\text{Sun}}r_{{\text{Earth}},{\text{Sun}}}^{-2}{\hat {\mathbf {r} }}_{{\text{Globe}},{\text{Sun}}}}$$

which is the dispatch of the Kepler motion. Then this Earth moves around the Dominicus according to Kepler'due south laws.

If the two bodies in the Solar System are Moon and Earth the acceleration of the Moon becomes

$${\displaystyle \mathbf {\ddot {r}} _{\text{Moon}}=Gm_{\text{Earth}}r_{{\text{Moon}},{\text{Earth}}}^{-2}{\hat {\mathbf {r} }}_{{\text{Moon}},{\text{World}}}}$$

And then in this approximation, the Moon moves effectually the Earth according to Kepler's laws.

In the three-torso case the accelerations are

$${\displaystyle {\begin{aligned}\mathbf {\ddot {r}} _{\text{Dominicus}}&=Gm_{\text{Earth}}r_{{\text{Dominicus}},{\text{Earth}}}^{-2}{\hat {\mathbf {r} }}_{{\text{Sun}},{\text{Earth}}}+Gm_{\text{Moon}}r_{{\text{Sun}},{\text{Moon}}}^{-2}{\hat {\mathbf {r} }}_{{\text{Sun}},{\text{Moon}}}\\\mathbf {\ddot {r}} _{\text{Earth}}&=Gm_{\text{Sun}}r_{{\text{Earth}},{\text{Lord's day}}}^{-2}{\hat {\mathbf {r} }}_{{\text{Earth}},{\text{Sun}}}+Gm_{\text{Moon}}r_{{\text{Earth}},{\text{Moon}}}^{-2}{\hat {\mathbf {r} }}_{{\text{World}},{\text{Moon}}}\\\mathbf {\ddot {r}} _{\text{Moon}}&=Gm_{\text{Sun}}r_{{\text{Moon}},{\text{Sun}}}^{-2}{\hat {\mathbf {r} }}_{{\text{Moon}},{\text{Lord's day}}}+Gm_{\text{World}}r_{{\text{Moon}},{\text{Earth}}}^{-2}{\chapeau {\mathbf {r} }}_{{\text{Moon}},{\text{World}}}\end{aligned}}}$$

These accelerations are not those of Kepler orbits, and the three-body trouble is complicated. But Keplerian approximation is the basis for perturbation calculations. (Run into Lunar theory.)

Position as a function of time [edit]

Kepler used his two commencement laws to compute the position of a planet as a function of time. His method involves the solution of a transcendental equation called Kepler's equation.

The process for calculating the heliocentric polar coordinates (r,θ) of a planet as a function of the time t since perihelion, is the following five steps:

1. Compute the mean motion n = (2π rad)/P , where P is the period.
2. Compute the hateful bibelot M = nt , where t is the fourth dimension since perihelion.
3. Compute the eccentric anomaly E by solving Kepler'south equation:

   $${\displaystyle M=E-\varepsilon \sin East,}$$

   

   where ${\displaystyle \varepsilon }$ is the eccentricity.
4. Compute the true anomaly θ past solving the equation:

   $${\displaystyle (i-\varepsilon )\tan ^{2}{\frac {\theta }{two}}=(1+\varepsilon )\tan ^{2}{\frac {E}{ii}}}$$

   

5. Compute the heliocentric distance r:

   $${\displaystyle r=a(i-\varepsilon \cos E),}$$

   

   where ${\displaystyle a}$ is the semimajor centrality.

The Cartesian velocity vector can then be calculated as ${\displaystyle \mathbf {v} ={\frac {\sqrt {\mu a}}{r}}\left\langle -\sin {E},{\sqrt {i-\varepsilon ^{two}}}\cos {E}\right\rangle }$ , where ${\displaystyle \mu }$ is the standard gravitational parameter.^[24]

The important special case of circular orbit, ε = 0, gives θ = Eastward = Thousand . Considering the uniform round motility was considered to be normal, a deviation from this motion was considered an anomaly.

The proof of this procedure is shown below.

Hateful anomaly, Grand [edit]

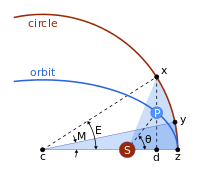
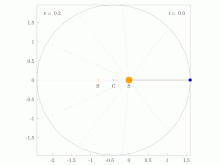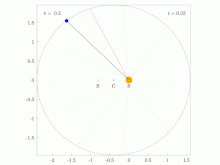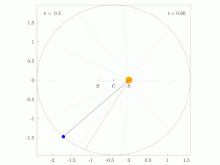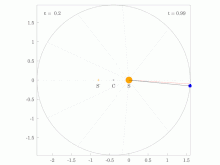
Figure five: Geometric construction for Kepler'south calculation of θ. The Sun (located at the focus) is labeled Due south and the planet P. The auxiliary circle is an aid to calculation. Line xd is perpendicular to the base of operations and through the planet P. The shaded sectors are arranged to accept equal areas by positioning of signal y.

The Keplerian problem assumes an elliptical orbit and the four points:

• due south the Sun (at ane focus of ellipse);
• z the perihelion
• c the center of the ellipse
• p the planet

and

• ${\displaystyle a=|cz|,}$ distance betwixt center and perihelion, the semimajor axis,
• ${\displaystyle \varepsilon ={|cs| \over a},}$ the eccentricity,
• ${\displaystyle b=a{\sqrt {ane-\varepsilon ^{2}}},}$ the semiminor axis,
• ${\displaystyle r=|sp|,}$ the distance between Sun and planet.
• ${\displaystyle \theta =\angle zsp,}$ the management to the planet as seen from the Lord's day, the truthful anomaly.

The problem is to compute the polar coordinates (r,θ) of the planet from the time since perihelion,t.

It is solved in steps. Kepler considered the circle with the major axis equally a diameter, and

The sector areas are related by ${\displaystyle |zsp|={\frac {b}{a}}\cdot |zsx|.}$

The round sector area ${\displaystyle |zcy|={\frac {a^{2}One thousand}{2}}.}$

The surface area swept since perihelion,

$${\displaystyle |zsp|={\frac {b}{a}}\cdot |zsx|={\frac {b}{a}}\cdot |zcy|={\frac {b}{a}}\cdot {\frac {a^{2}M}{2}}={\frac {abM}{2}},}$$

is past Kepler's 2d law proportional to fourth dimension since perihelion. And then the mean anomaly, M, is proportional to time since perihelion, t.

$${\displaystyle M=nt,}$$

where n is the mean motion.

Eccentric anomaly, E [edit]

When the mean anomaly One thousand is computed, the goal is to compute the truthful anomaly θ. The function θ =f(Grand) is, however, not elementary.^[25] Kepler'due south solution is to use

$${\displaystyle Eastward=\angle zcx,}$$

10 as seen from the centre, the eccentric anomaly as an intermediate variable, and kickoff compute E as a function of M past solving Kepler'due south equation below, and then compute the truthful anomaly θ from the eccentric anomaly E. Here are the details.

$${\displaystyle {\brainstorm{aligned}|zcy|&=|zsx|=|zcx|-|scx|\\{\frac {a^{2}Yard}{ii}}&={\frac {a^{2}E}{2}}-{\frac {a\varepsilon \cdot a\sin Eastward}{2}}\end{aligned}}}$$

Partition by a ²/2 gives Kepler'southward equation

$${\displaystyle M=Due east-\varepsilon \sin E.}$$

This equation gives K as a function of Due east. Determining East for a given Chiliad is the inverse problem. Iterative numerical algorithms are commonly used.

Having computed the eccentric anomaly Due east, the next pace is to calculate the true anomalyθ.

Merely note: Cartesian position coordinates with reference to the heart of ellipse are (a cosE,b sinEast)

With reference to the Sun (with coordinates (c,0) = (ae,0) ), r = (a cosEast – ae, b sinE)

Truthful bibelot would be arctan(r _y/r x), magnitude of r would be √ r ·r .

Truthful anomaly, θ [edit]

Annotation from the figure that

$${\displaystyle {\overrightarrow {cd}}={\overrightarrow {cs}}+{\overrightarrow {sd}}}$$

so that

$${\displaystyle a\cos E=a\varepsilon +r\cos \theta .}$$

Dividing by ${\displaystyle a}$ and inserting from Kepler's first law

$${\displaystyle {\frac {r}{a}}={\frac {1-\varepsilon ^{2}}{ane+\varepsilon \cos \theta }}}$$

to get

$${\displaystyle \cos E=\varepsilon +{\frac {1-\varepsilon ^{2}}{1+\varepsilon \cos \theta }}\cos \theta ={\frac {\varepsilon (ane+\varepsilon \cos \theta )+\left(1-\varepsilon ^{2}\right)\cos \theta }{ane+\varepsilon \cos \theta }}={\frac {\varepsilon +\cos \theta }{1+\varepsilon \cos \theta }}.}$$

The result is a usable relationship between the eccentric bibelot E and the true anomalyθ.

A computationally more convenient form follows by substituting into the trigonometric identity:

$${\displaystyle \tan ^{2}{\frac {10}{two}}={\frac {1-\cos 10}{1+\cos x}}.}$$

Get

$${\displaystyle {\brainstorm{aligned}\tan ^{2}{\frac {East}{two}}&={\frac {1-\cos Eastward}{1+\cos E}}={\frac {1-{\frac {\varepsilon +\cos \theta }{1+\varepsilon \cos \theta }}}{one+{\frac {\varepsilon +\cos \theta }{1+\varepsilon \cos \theta }}}}\\[8pt]&={\frac {(i+\varepsilon \cos \theta )-(\varepsilon +\cos \theta )}{(ane+\varepsilon \cos \theta )+(\varepsilon +\cos \theta )}}={\frac {ane-\varepsilon }{1+\varepsilon }}\cdot {\frac {one-\cos \theta }{1+\cos \theta }}={\frac {ane-\varepsilon }{1+\varepsilon }}\tan ^{2}{\frac {\theta }{two}}.\end{aligned}}}$$

Multiplying by 1 +ε gives the event

$${\displaystyle (1-\varepsilon )\tan ^{two}{\frac {\theta }{2}}=(i+\varepsilon )\tan ^{ii}{\frac {E}{ii}}}$$

This is the tertiary pace in the connection between time and position in the orbit.

Distance, r [edit]

The fourth pace is to compute the heliocentric distance r from the true anomaly θ by Kepler'south starting time constabulary:

$${\displaystyle r(1+\varepsilon \cos \theta )=a\left(ane-\varepsilon ^{two}\right)}$$

Using the relation above betwixt θ and E the final equation for the distance r is:

$${\displaystyle r=a(1-\varepsilon \cos E).}$$

See besides [edit]

• Circular motion
• Free-fall time
• Gravity
• Kepler orbit
• Kepler problem
• Kepler'southward equation
• Laplace–Runge–Lenz vector
• Specific relative angular momentum, relatively easy derivation of Kepler's laws starting with conservation of angular momentum

Explanatory notes [edit]

1. ^ In 1621, Johannes Kepler noted that Jupiter's moons obey (approximately) his third police in his Epitome Astronomiae Copernicanae [Paradigm of Copernican Astronomy] (Linz ("Lentiis ad Danubium"), (Republic of austria): Johann Planck, 1622), book iv, part ii, pages 554–555. From pp. 554–555: " ... plane ut est cum sexual activity planet circa Solem, ... prodit Marius in suo mundo Ioviali ista 3.5.8.13 (vel xiv. Galilæo) ... Periodica vero tempora prodit idem Marius ... sunt maiora simplis, minora vero duplis." (... only as information technology is clearly [truthful] amid the half-dozen planets around the Sun, so also it is among the four [moons] of Jupiter, considering around the torso of Jupiter any [satellite] that can go farther from it, orbits slower, and even that [orbit's period] is not in the same proportion, only greater [than the distance from Jupiter]; that is, iii/2 (sescupla) of the proportion of each of the distances from Jupiter, which is clearly the very [proportion] as is used for the half dozen planets above. In his [book] The World of Jupiter [Mundus Jovialis, 1614], [Simon Mayr or] "Marius" [1573–1624] presents these distances, from Jupiter, of the four [moons] of Jupiter: 3, 5, 8, 13 (or fourteen [co-ordinate to] Galileo) [Annotation: The distances of Jupiter'southward moons from Jupiter are expressed as multiples of Jupiter's diameter.] ... Mayr presents their fourth dimension periods: 1 twenty-four hours eighteen 1/2 hours, 3 days thirteen 1/3 hours, vii days two hours, 16 days 18 hours: for all [of these data] the proportion is greater than double, thus greater than [the proportion] of the distances three, five, eight, 13 or 14, although less than [the proportion] of the squares, which double the proportions of the distances, namely 9, 25, 64, 169 or 196, just equally [a power of] 3/two is also greater than 1 but less than 2.)
2. ^ Godefroy Wendelin wrote a letter to Giovanni Battista Riccioli about the relationship between the distances of the Jovian moons from Jupiter and the periods of their orbits, showing that the periods and distances conformed to Kepler's third police force. Come across: Joanne Baptista Riccioli, Almagestum novum ... (Bologna (Bononia), (Italian republic): Victor Benati, 1651), book 1, page 492 Scholia Iii. In the margin beside the relevant paragraph is printed: Vendelini ingeniosa speculatio circa motus & intervalla satellitum Jovis. (Wendelin's clever speculation about the movement and distances of Jupiter's satellites.) From p. 492: "Iii. Not minus Kepleriana ingeniosa est Vendelini ... & D. seven. 164/k. pro penextimo, & D. xvi. 756/1000. pro extimo." (No less clever [than] Kepler'due south is the almost great astronomer Wendelin'southward investigation of the proportion of the periods and distances of Jupiter's satellites, which he had communicated to me with great generosity [in] a very long and very learned letter. So, just as in [the case of] the larger planets, the planets' mean distances from the Sunday are respectively in the 3/2 ratio of their periods ; then the distances of these minor planets of Jupiter from Jupiter (which are 3, 5, viii, and xiv) are respectively in the 3/2 ratio of [their] periods (which are 1.769 days for the innermost [Io], 3.554 days for the next to the innermost [Europa], 7.164 days for the adjacent to the outermost [Ganymede], and 16.756 days for the outermost [Callisto]).)

Citations [edit]

1. ^ Voltaire, Eléments de la philosophie de Newton [Elements of Newton's Philosophy] (London, England: 1738). Come across, for example:
   • From p. 162: "Par une des grandes loix de Kepler, toute Planete décrit des aires égales en temp égaux : par une autre loi non-moins sûre, chaque Planete fait sa révolution autour du Soleil en telle sort, que si, sa moyenne distance au Soleil est 10. prenez le cube de ce nombre, ce qui sera g., & le tems de la révolution de cette Planete autour du Soleil sera proportionné à la racine quarrée de ce nombre 1000." (By 1 of the great laws of Kepler, each planet describes equal areas in equal times ; past some other law no less certain, each planet makes its revolution effectually the sun in such a way that if its mean distance from the sun is ten, take the cube of that number, which will be 1000, and the time of the revolution of that planet around the dominicus will be proportional to the foursquare root of that number thou.)
   • From p. 205: "Il est donc prouvé par la loi de Kepler & par celle de Neuton, que chaque Planete gravite vers le Soleil, ... " (It is thus proved past the law of Kepler and by that of Newton, that each planet revolves around the sun ... )
2. ^ ^{a b} Wilson, Curtis (May 1994). "Kepler'southward Laws, And then-Chosen" (PDF). HAD News (31): i–2. Retrieved December 27, 2016.
3. ^ De la Lande, Astronomie, vol. 1 (Paris, France: Desaint & Saillant, 1764). See, for example:
   • From page 390: " ... mais suivant la fameuse loi de Kepler, qui sera expliquée dans le Livre suivant (892), le rapport des temps périodiques est toujours plus grand que celui des distances, une planete cinq fois plus éloignée du soleil, emploie à faire sa révolution douze fois plus de temps ou environ; ... " ( ... but according to the famous police of Kepler, which will be explained in the post-obit book [i.due east., affiliate] (paragraph 892), the ratio of the periods is e'er greater than that of the distances [then that, for example,] a planet v times farther from the sun, requires about twelve times or then more time to make its revolution [around the sun] ... )
   • From page 429: "Les Quarrés des Temps périodiques sont comme les Cubes des Distances. 892. La plus fameuse loi du mouvement des planetes découverte par Kepler, est celle du repport qu'il y a entre les grandeurs de leurs orbites, & le temps qu'elles emploient à les parcourir; ... " (The squares of the periods are as the cubes of the distances. 892. The about famous law of the motion of the planets discovered by Kepler is that of the relation betwixt the sizes of their orbits and the times that the [planets] require to traverse them; ... )
   • From page 430: "Les Aires sont proportionnelles au Temps. 895. Cette loi générale du mouvement des planetes devenue si importante dans 50'Astronomie, sçavior, que les aires sont proportionnelles au temps, est encore une des découvertes de Kepler; ... " (Areas are proportional to times. 895. This general law of the movement of the planets [which has] become then important in astronomy, namely, that areas are proportional to times, is one of Kepler'due south discoveries; ... )
   • From folio 435: "On a appellé cette loi des aires proportionnelles aux temps, Loi de Kepler, aussi bien que celle de l'article 892, du nome de ce célebre Inventeur; ... " (One called this law of areas proportional to times (the law of Kepler) also as that of paragraph 892, by the name of that celebrated inventor; ... )
4. ^ Robert Small, An account of the astronomical discoveries of Kepler (London, England: J Mawman, 1804), pp. 298–299.
5. ^ Robert Modest, An account of the astronomical discoveries of Kepler (London, England: J. Mawman, 1804).
6. ^ Bruce Stephenson (1994). Kepler's Physical Astronomy. Princeton University Press. p. 170. ISBN978-0-691-03652-6.
7. ^ Astronomia nova Aitiologitis, seu Physica Coelestis tradita Commentariis de Motibus stellae Martis ex observationibus G.V. Tychnonis.Prague 1609; Engl. tr. W.H. Donahue, Cambridge 1992.
8. ^ In his Astronomia nova, Kepler presented merely a proof that Mars' orbit is elliptical. Testify that the other known planets' orbits are elliptical was presented merely in 1621.
   See: Johannes Kepler, Astronomia nova ... (1609), p. 285. After having rejected circular and oval orbits, Kepler concluded that Mars' orbit must be elliptical. From the top of page 285: "Ergo ellipsis est Planetæ iter; ... " (Thus, an ellipse is the planet's [i.e., Mars'] path; ... ) After the aforementioned page: " ... ut sequenti capite patescet: ubi simul etiam demonstrabitur, nullam Planetæ relinqui figuram Orbitæ, præterquam perfecte ellipticam; ... " ( ... as will exist revealed in the next chapter: where information technology will likewise so be proved that any figure of the planet's orbit must be relinquished, except a perfect ellipse; ... ) And then: "Caput LIX. Demonstratio, quod orbita Martis, ... , fiat perfecta ellipsis: ... " (Chapter 59. Proof that Mars' orbit, ... is a perfect ellipse: ... ) The geometric proof that Mars' orbit is an ellipse appears as Protheorema XI on pages 289–290.
   Kepler stated that every planet travels in elliptical orbits having the Dominicus at one focus in: Johannes Kepler, Paradigm Astronomiae Copernicanae [Summary of Copernican Astronomy] (Linz ("Lentiis ad Danubium"), (Austria): Johann Planck, 1622), book 5, part 1, 3. De Figura Orbitæ (III. On the effigy [i.e., shape] of orbits), pages 658–665. From p. 658: "Ellipsin fieri orbitam planetæ ... " (Of an ellipse is fabricated a planet'southward orbit ... ). From p. 659: " ... Sole (Foco altero huius ellipsis) ... " ( ... the Sun (the other focus of this ellipse) ... ).
9. ^ ^{a b} Holton, Gerald James; Castor, Stephen Grand. (2001). Physics, the Human Adventure: From Copernicus to Einstein and Beyond (3rd paperback ed.). Piscataway, NJ: Rutgers University Press. pp. 40–41. ISBN978-0-8135-2908-0 . Retrieved December 27, 2009.
10. ^ In his Astronomia nova ... (1609), Kepler did not present his second constabulary in its modern form. He did that only in his Epitome of 1621. Furthermore, in 1609, he presented his second law in two different forms, which scholars call the "distance law" and the "expanse police".
    • His "distance police" is presented in: "Caput XXXII. Virtutem quam Planetam movet in circulum attenuari cum discessu a fonte." (Affiliate 32. The force that moves a planet circularly weakens with distance from the source.) See: Johannes Kepler, Astronomia nova ... (1609), pp. 165–167. On page 167, Kepler states: " ... , quanto longior est αδ quam αε, tanto diutius moratur Planeta in certo aliquo arcui excentrici apud δ, quam in æquali arcu excentrici apud ε." ( ... , as αδ is longer than αε, so much longer will a planet remain on a sure arc of the eccentric near δ than on an equal arc of the eccentric near ε.) That is, the farther a planet is from the Sun (at the betoken α), the slower it moves along its orbit, so a radius from the Sun to a planet passes through equal areas in equal times. Still, as Kepler presented it, his statement is accurate only for circles, not ellipses.
    • His "area constabulary" is presented in: "Caput LIX. Demonstratio, quod orbita Martis, ... , fiat perfecta ellipsis: ... " (Chapter 59. Proof that Mars' orbit, ... , is a perfect ellipse: ... ), Protheorema XIV and XV, pp. 291–295. On the top p. 294, it reads: "Arcum ellipseos, cujus moras metitur area AKN, debere terminari in LK, ut sit AM." (The arc of the ellipse, of which the duration is delimited [i.due east., measured] by the expanse AKM, should exist terminated in LK, so that it [i.east., the arc] is AM.) In other words, the time that Mars requires to movement forth an arc AM of its elliptical orbit is measured by the area of the segment AMN of the ellipse (where N is the position of the Sun), which in turn is proportional to the section AKN of the circle that encircles the ellipse and that is tangent to information technology. Therefore, the area that is swept out by a radius from the Sun to Mars every bit Mars moves along an arc of its elliptical orbit is proportional to the time that Mars requires to movement along that arc. Thus, a radius from the Lord's day to Mars sweeps out equal areas in equal times.
    In 1621, Kepler restated his second law for any planet: Johannes Kepler, Epitome Astronomiae Copernicanae [Summary of Copernican Astronomy] (Linz ("Lentiis advertizement Danubium"), (Austria): Johann Planck, 1622), book 5, page 668. From page 668: "Dictum quidem est in superioribus, divisa orbita in particulas minutissimas æquales: accrescete iis moras planetæ per eas, in proportione intervallorum inter eas & Solem." (It has been said above that, if the orbit of the planet is divided into the smallest equal parts, the times of the planet in them increase in the ratio of the distances between them and the sunday.) That is, a planet'south speed forth its orbit is inversely proportional to its altitude from the Sun. (The remainder of the paragraph makes clear that Kepler was referring to what is at present called angular velocity.)
11. ^ ^{a b} Johannes Kepler, Harmonices Mundi [The Harmony of the Earth] (Linz, (Republic of austria): Johann Planck, 1619), book five, chapter iii, p. 189. From the bottom of p. 189: "Sed res est certissima exactissimaque quod proportio qua est inter binorum quorumcunque Planetarum tempora periodica, sit præcise sesquialtera proportionis mediarum distantiarum, ... " (But it is absolutely certain and exact that the proportion between the periodic times of any two planets is precisely the sesquialternate proportion [i.due east., the ratio of three:ii] of their mean distances, ... ")
    An English language translation of Kepler'south Harmonices Mundi is available as: Johannes Kepler with Due east. J. Aiton, A. M. Duncan, and J. V. Field, trans., The Harmony of the World (Philadelphia, Pennsylvania: American Philosophical Lodge, 1997); see especially p. 411.
12. ^ National Globe Science Teachers Association (nine Oct 2008). "Information Table for Planets and Dwarf Planets". Windows to the Universe . Retrieved two August 2018.
13. ^ Mercator, Nicolaus (1664). Nicolai Mercatoris Hypothesis astronomica nova, et consensus eius cum observationibus [Nicolaus Mercator'due south new astronomical hypothesis, and its agreement with observations] (in Latin). London, England: Leybourn.
14. ^ Mercator, Nic. (25 March 1670). "Some considerations of Mr. Nic. Mercator, concerning the geometrick and directly method of signior Cassini for finding the apogees, excentricities, and anomalies of the planets; ..." Philosophical Transactions of the Imperial Society of London (in Latin). 5 (57): 1168–1175. doi:10.1098/rstl.1670.0018. Mercator criticized Cassini's method of finding, from three observations, an orbit'south line of apsides. Cassini had assumed (wrongly) that planets move uniformly along their elliptical orbits. From p. 1174: "Sed cum id Observationibus nequaquam congruere animadverteret, mutavit sententiam, & lineam veri motus Planetæ æqualibus temporibus æquales areas Ellipticas verrere professus est: ... " (But when he noticed that it didn't agree at all with observations, he changed his thinking, and he declared that a line [from the Sunday to a planet, cogent] a planet's true motion, sweeps out equal areas of an ellipse in equal periods of time: ... [which is the "area" class of Kepler'southward second law])
15. ^ Wilbur Applebaum (2000). Encyclopedia of the Scientific Revolution: From Copernicus to Newton. Routledge. p. 603. Bibcode:2000esrc.book.....A. ISBN978-1-135-58255-5.
16. ^ Roy Porter (1992). The Scientific Revolution in National Context . Cambridge University Press. p. 102. ISBN978-0-521-39699-8.
17. ^ Victor Guillemin; Shlomo Sternberg (2006). Variations on a Theme by Kepler. American Mathematical Soc. p. 5. ISBN978-0-8218-4184-half dozen.
18. ^ Bryant, Jeff; Pavlyk, Oleksandr. "Kepler's 2nd Law", Wolfram Demonstrations Project. Retrieved December 27, 2009.
19. ^ Burtt, Edwin. The Metaphysical Foundations of Modern Physical Scientific discipline. p. 52.
20. ^ Gerald James Holton, Stephen G. Brush (2001). Physics, the Homo Adventure. Rutgers University Printing. p. 45. ISBN978-0-8135-2908-0.
21. ^ Caspar, Max (1993). Kepler . New York: Dover. ISBN9780486676050.
22. ^ I. Newton, Principia, p. 408 in the translation of I.B. Cohen and A. Whitman
23. ^ I. Newton, Principia, p. 943 in the translation of I.B. Cohen and A. Whitman
24. ^ Schwarz, René. "Memorandum № 1: Keplerian Orbit Elements → Cartesian Country Vectors" (PDF) . Retrieved 4 May 2018.
25. ^ Müller, M (1995). "Equation of Time – Problem in Astronomy". Acta Physica Polonica A. Retrieved 23 February 2013.

General bibliography [edit]

• Kepler'due south life is summarized on pages 523–627 and Volume 5 of his magnum opus, Harmonice Mundi (harmonies of the world), is reprinted on pages 635–732 of On the Shoulders of Giants: The Great Works of Physics and Astronomy (works by Copernicus, Kepler, Galileo, Newton, and Einstein). Stephen Hawking, ed. 2002 ISBN 0-7624-1348-four
• A derivation of Kepler's third constabulary of planetary motion is a standard topic in engineering mechanics classes. See, for case, pages 161–164 of Meriam, J.L. (1971) [1966]. Dynamics, 2nd ed. New York: John Wiley. ISBN978-0-471-59601-i. .
• Murray and Dermott, Solar System Dynamics, Cambridge University Press 1999, ISBN 0-521-57597-4
• V. I. Arnold, Mathematical Methods of Classical Mechanics, Chapter 2. Springer 1989, ISBN 0-387-96890-three

External links [edit]

• B.Surendranath Reddy; animation of Kepler'due south laws: applet
• "Derivation of Kepler'southward Laws" (from Newton's laws) at Physics Stack Substitution.
• Crowell, Benjamin, Low-cal and Matter, an online book that gives a proof of the outset law without the utilize of calculus (encounter department 15.7)
• David McNamara and Gianfranco Vidali, Kepler's Second Constabulary – Coffee Interactive Tutorial, https://web.archive.org/spider web/20060910225253/http://www.phy.syr.edu/courses/java/mc_html/kepler.html, an interactive Java applet that aids in the understanding of Kepler's Second Law.
• Audio – Cain/Gay (2010) Astronomy Cast Johannes Kepler and His Laws of Planetary Motility
• University of Tennessee'due south Dept. Physics & Astronomy: Astronomy 161 page on Johannes Kepler: The Laws of Planetary Motion [1]
• Equant compared to Kepler: interactive model [two]
• Kepler's Third Law:interactive model [3]
• Solar System Simulator (Interactive Applet)
• Kepler and His Laws, educational web pages by David P. Stern

How To Describe The Moon,

Source: https://en.wikipedia.org/wiki/Kepler%27s_laws_of_planetary_motion

Posted by: godwinaces1963.blogspot.com

Share this post